En jouant à faire des agrandissements ou réductions à la photocopieuse, vous avez sans doute déjà remarqué qu'on peut réduire deux A4 (ou un A3) en un A4 de manière exacte, sans marges ni rognage, et de même, on peut agrandir un A5 en A4 de manière exacte.
Essayez de faire cela avec un rectangle d'une autre forme (par exemple un rectangle dont les côtés sont dans un rapport 1:2, un carré ou même une feuille au format US Letter mesurant 8,5 pouces sur 11 pouces), vous n'y arriverez pas.
D'où vient donc cette propriété si utile du format A4 ?
Sommets alignés
Une autre expérience avant de se lancer dans les maths. Prenez deux feuilles A4. Gardez la première intacte. Coupez l'autre en deux selon la petite médiane, cela vous donne deux A5. Gardez un A5 intact et coupez l'autre A5 en deux A6. Gardez un A6 et coupez l'autre en deux A7, et ainsi de suite. Disposez les rectangles A4, A5, A6, A7, ... les uns sur les autres, comme sur une des figures suivantes.
Des rectangles semblables
De ces deux expériences, on peut comprendre la propriété des formats de papier A3, A4, A5, ... Quand la feuille est pliée en deux le long de sa petite médiane, le rectangle obtenu est semblable, au sens géométrique du terme, au rectangle initial. Cela veut dire que les côtés du rectangle initial et du rectangle plié sont dans un même rapport.Recherche du rapport longueur / largeur d'une feuille A4
On peut chercher le rapport entre la longueur et la largeur des feuilles de format A4, A3, ...
Avec les notations de la figure ci-contre, et sachant que les deux rectangles sont semblables, on peut écrire
\[\frac{L}{\ell}=\frac{\ell}{L/2}.\]
On en déduit que le rapport $L/\ell$ vaut $\sqrt{2}$. Ainsi, si par exemple $\ell$ est la largeur d'un A4 et $L$ sa longueur, on a $L=\sqrt{2}\,\ell$.
Le papier A4, mais également tous les papiers de format A (A0, A1, A2, A3, ...) ont donc des côtés dans un rapport $1:\sqrt{2}$. En anglais, un rectangle dont les côtés sont dans ce rapport est appelé Silver rectangle.
Recherche des dimensions exactes d'une feuille A4
On peut rechercher les dimensions exactes d'un A4, sachant que l'A0 a été choisi pour avoir une aire de 1 m² et que deux A1 équivalent à un A0 et ainsi de suite, ce qui signifie qu'on peut placer exactement 16 feuilles A4 dans un A0. |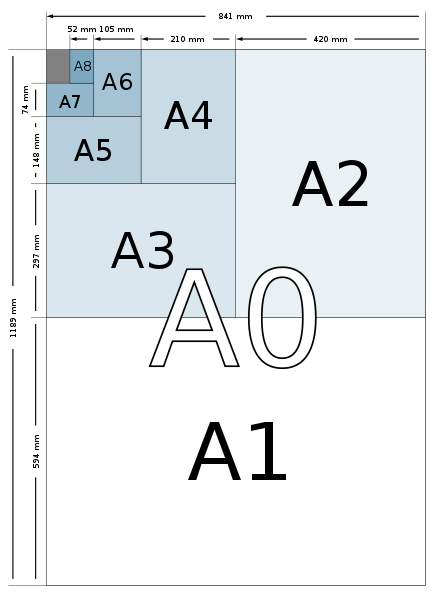
| Formats de papier A - Source de l'image : Wikipedia |
Format A4 et origami
De nombreux pliages exploitent les propriétés particulières du format A4. Nous en présenterons quelques uns sur ce blog.Pour les lecteurs impatients et prêts à affronter des pliages relativement difficiles, je peux conseiller l'ouvrage de Jun Maekawa, Genuine Japanese Origami. 34 Mathematical Models based upon $\sqrt{2}$.
Bibliographie
- Jun Maekawa, Genuine Japanese Origami. 34 Mathematical Models based upon $\sqrt{2}$. Book 2, Dover Publications, 2012.
- Patricia Wantiez et Laure Ninove, Exploiter le pliage pour démontrer au milieu du secondaire, Revue Losanges, n.20, SBPMef, mars 2013, pp. 32-42.
Aucun commentaire:
Enregistrer un commentaire